انجام پروژه متلب فازی سیستم های خبره منطق فازی
برای انجام پروژه متلب فازی سیستم های خبره منطق فازی (Fuzzy Logic Matlab) با بهترین کیفیت و زمان و هزینه همراه با آموزش با شماره ۰۹۱۹۰۰۹۰۲۵۸ در ارتباط باشید.
تئوری منطق فازی
تئوری مجموعه های فازی برای سر و کار داشتن با مفهوم رتبه بندی ارزش واقعیت جزئی از کاملا درست تا کاملا غلط،توسعه داده شده است. تئوری مجموعه فازی به ابزار برجسته ای برای سر و کار داشتن با عدم دقت و تعیین ابهام در اندازه،ایجاد راه حل های قدرتمند و با حداقل هزینه برای مسائل دنیا واقعی، تبدیل شده است. برا ساس گفته های زاده (۱۹۷۵) نشان دادن معقول وضعیت های پیچیده توسط متغیرهای کمی قراردادی سخت است و ضروری است که از متغیرهای زبانی که ارزش آنها بوسیله کلمات یا جملاتی که به صورت زبان طبیعی یا ساختگی بیان می شوند، نشان داده می شود. ویژگیهایی مانند پتانسیل کار کردن با متغیرهای زبانی،هزینه پایین محاسبات و سهولت درک و فهم آن، باعث شهرت این رویکرد شده است. جبر تئوری فازی توسعه داده شده توسط زاده(۱۹۶۵) ساختار رسمی تئوری می باشد که به راه حل عدم دقت و ابهام در محیط های نامشخص اجازه برآورد می دهد.
هنگام بکار گیری این تئوری برای حل مسائل اندازه گیری عملکرد یا پیش بینی،منطق فازی از متخصص حوزه دانش مربوطه کمک گرفته و با استفاده از حساب فازی سیستم های استنتاج فازی تولید می کند. منطق فازی ابزاری از تئوری مجموعه فازی می باشد که به طور خاص برای سر و کار داشتن با اطلاعات مبهم فرایند با تابع عضویت متغیر بکار می رود. عملکرد فازی یک فرایند”حلقه-فازی-حلقه”برای یک سیستم واقعی که ورودی اصلی و خروجی نهایی آن ها باید متغیرهای حلقه ای باشند، اما فرایند واسطه ای(میانه) یک فرایند استنتاجی فازی می باشد. استنتاج فازی روشی است که ارزش بردار ورودی را تفسیر می کند و بوسیله ابزارهای برخی مجموعه های قواعد فازی، به خروجی ارزش تخصیص می دهد. در مجموعه سنتی،یک عامل یا متعلق به مجموعه است یا متعلق به مجموعه نیست.
عدد فازی، یک مجموعه فازی روی R (اعداد حقیقی) است که حداقل سه شرط زیر را ارضا نماید.
باید یک مجموعه فازی نرمال باشد.
باید یک بازه بسته روی هر مقدار باشد.
مجموعه پشتیبان باید محدود باشد.
از آنجایی که هر برش از هر عدد فازی باید یک بازه بسته باشد در نتیجه هر عدد فازی یک مجموعه فازی محدب می باشد. البته عکس این مطلب لزوما صادق نیست.
اشکال معروف و پرکاربرد اعداد فازی عبارتند از :
عدد فازی مثلثی
عدد فازی ذوزنقه ای
عدد فازی گوسی
عدد فازی زنگوله ای
عدد فازی سیگمویدال افزایشی یا کاهشی
اعداد فازی نقش مهمی در فرموله کردن کمی متغیرهای فازی دارند. متغیرهای فازی می توانند متغیرهای کلامی و اعداد فازی بیانگر متغیرهای کلامی باشند. متغیرهای کلامی به مفاهیم کلامی مانند، خیلی کوچک، متوسط، بزرگ و … گفته می شود. به عنوان مثال از متغیرهای کلامی به شکل(۱-۲) توجه نمائید.
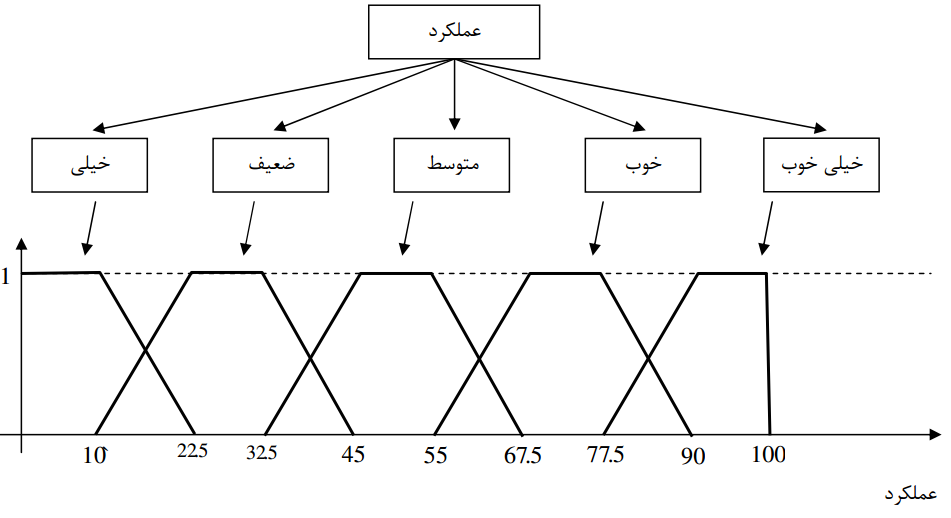
نمونه ای از متغیرهای کلامی در بیان عملکرد
در تعیین تابع عضویت متغیرهای کلامی، یکی از متغیرها به عنوان متغیر پایه فرض شده و تابع عضویت برای آن متغیر تعیین می شود. سپس تابع عضویت سایر مقادیر کلامی با استفاده از فرمولهایی بدست می آید. به عنوان مثال فرض کنید مقدار کلامی به عنوان متغیر پایه در نظر گرفته شود. آنگاه سایر مقادیر کلامی می توانند بصورت ذیل بدست می آیند. نمایش شماتیک اشکال مختلف متغیرهای کلامی در شکل زیر آمده است.
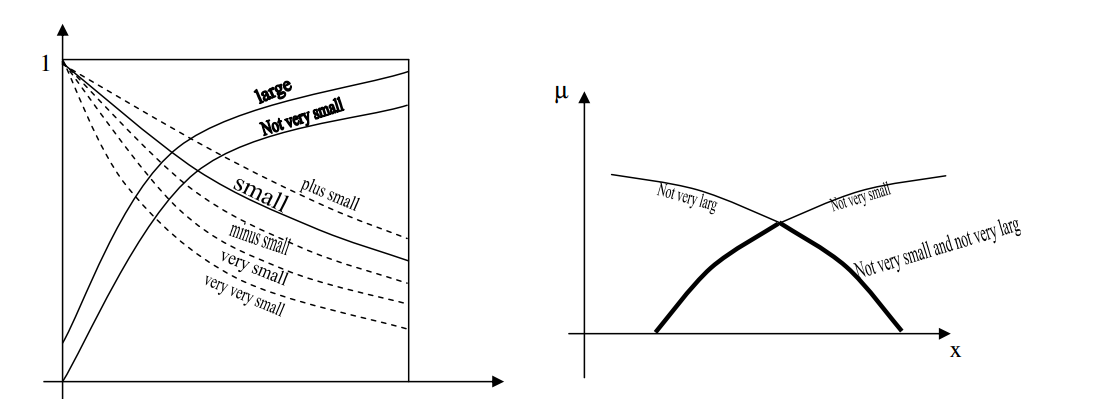
اشکال مختلف تابع عضویت متغیرهای کلامی
عملیات ریاضی بر روی اعداد فازی
فرض کنید علامت * بیانگر هر یک از چهار عمل اصلی ریاضی باشد و دو عدد فازی روی مجموعه اعداد حقیقی تعریف شده است. آنگاه معادله بصورت ذیل تعریف می شود. در نتیجه برای چهار عمل اصلی ریاضی در اعداد فازی خواهیم داشت.
بکارگیری اطلاعات فازی در تصمیم گیری، محاسبات و مدلسازی با پیاده سازی نتایج فازی در دنیای واقعی تفاوت دارد. علیرغم اینکه بسیاری از اطلاعات که هر روز انسانها با آنها سرو کار دارند فازی هستند، بسیاری از اقدامات یا تصمیماتی که اتخاذ و پیاده می شوند قطعی است. تصمیماتی که توسط ما اتخاذ می شوند، سخت افزارها و کامپیوترهایی که استفاده می کنیم، همگی بر اساس نظریه باینری (دودوئی) عمل می کنند. به عنوان مثال اگر می خواهیم بر روی تولید یک محصول جدید تصمیم گیری کنیم دو حالت وجود دارد، یا تولید می کنیم و یا تولید نمی کنیم، نمی توانیم بگوییم که تقریبا تولید می کنیم. لذا جاییکه تحلیل و محاسبات با اطلاعات فازی انجام می شوند و یا یک مدلی بر اساس ساختار فازی و اطلاعات ورودی فازی ایجاد می شود یا باید محاسبات و مدل طوری عمل نماید که خروجی آن که یک تصمیم و یا اقدام قطعی باشد (البته نه در همه موارد، بلکه در مواردی که ماهیت تصمیم حکم می کند که باید قطعی باشد) و یا اینکه با اعمال یکسری عملگرهایی نتیجه فازی به نتیجه کلاسیک تبدیل شود.
در این بخش راههای مختلف تبدیل یک مجموعه فازی به یک مجموعه کلاسیک و یا به یک مقدار (ارزش) واحد بررسی می شوند.
در این بخش روشهای مختلف تبدیل یک مجموعه (عدد) فازی به یک مجموعه (عدد) کلاسیک تشریح می گردند.
برای یک مجموعه فازی ، مجموعه برش که نشان داده می شود یک مجموعه کلاسیک است و اعضاء آن، اعضایی هستند که درجه عضویت آنها در مجموعه فازی ، بزرگتر یا مساوی می باشد.
توجه داشته باشید که مجموعه برش ، یک مجموعه با درجه پایین نیست، بلکه یک مجموعه کلاسیک است که از مجموعه فازی والد مشتق می شود.
به این روش، روش ارتفاع نیز گفته می شود. در این روش یک مجموعه (عدد) فازی تبدیل به یک عدد کلاسیک که بیشترین درجه عضویت را در مجموعه (عدد) فازی دارد، می شود.
این روش که روش مرکز ناحیه نیز نام دارد بیشترین کاربرد را نسبت به سایر روشها دارد. و به شرح زیر می باشد :
این روش صرفا برای مجموعه (عدد) فازی با تابع عضویت متقارن معتبر است و به شرح زیر می باشد.
این روش که به نام ” میانه حداکثر” نیز معروف است خیلی نزدیک به روش اول می باشد. البته به غیر از حالتی که ناحیه حداکثر محدود به یک نقطه نیست.
خانه متلب اولین و بهترین سایت در زمینه انجام پروژه های متلب است. در خانه متلب هیچ گونه واسطه ای وجود ندارد و به صورت مستقیم می توانید با مجری در ارتباط باشید.

